Information Transportation versus Transformation [Part 1]
Exploring the fascination with information theory and its connection to communications and technology.
Every year I take a trip out to Montana to teach at a weekend seminar series that's part of the University of Montana's Entertainment Management. I'm 11 years in and I work really hard to create original content for each year. This time around I talked about mental models, theories of communications and information, and a bit about machine learning. I wanted to try to take a bit of the content I shared there and repurpose it. As always, you can subscribe by email here.
The article I've shared more than any other this year is this Aeon piece by Jimmy Soni and Rob Goodman about Claude Shannon, the father of information theory. I knew basically nothing about information theory before reading this and have since consumed just about everything I could find on the topic. I wanted to talk a bit about why information theory fascinated me and also tie it to my broader interest in communications studies generally and McLuhan specifically.
Shannon and McLuhan were two of the most important thinkers of the 20th century. Without Shannon we'd have no computers and without McLuhan we wouldn't examine the effects of media, communications, and technology on society with the urgency we do. With that said, they're very different in their science and approach. Shannon was fundamentally a mathematician while McLuhan was a scholar of literature. In their work Shannon examined huge questions around how communications works technically, while McLuhan examined how it works tactically. When asked, McLuhan drew the distinction as questions of "transportation" versus "transformation":
I want to take some time to go through both, as they are fascinating in their own ways.
So now imagine we put all our letters (and a space) in a hat. But instead of 1 letter each, we have 100 total tiles in the hat and they alight with the chart above: 13 tiles for “e”, 4 tiles for “d”, 1 tile for “v”. Here’s what Shannon got when he did this:
OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL
He called this “first-order approximation” and while it still doesn’t make much sense, it’s a lot less random than the first example.
What’s wrong with that last example is that letters don’t operate independently. Let’s play a game for a second. I’m going to say a letter and you guess the next one. If I say “T” the odds are most of you are going to say “H”. That makes lots of sense since “the” is the most popular word in the English language. So instead of just picking letters at random based on probability what Shannon did next is pick one letter and then match it with it’s probabilistic pair. These are called bigrams and just like we had letter frequencies, we can chart these out.
This time Shannon took a slightly different approach. Rather than loading up a bunch of bigrams in a hat and picking them out at random he turned to a random page in a book and choose a random letter. He then turned to another random page in the same book and found the first occurance of recorded the letter immediately after it. What came out starts to look a lot more like English:
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TUCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE
Now I’m guessing you’re starting to see the pattern here. Next Shannon looked at trigrams, sets of three letters.
For his “third-order approximation” he once again uses the book but goes three letters deep:
IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE
He could go on and on and it would become closer and closer to English. Instead he switches to words, which also occur probabilistically.
For his “first-order approximation” he picks random words from the book. It looks a lot like a sentence because words don’t occur randomly. There’s a good chance an “and” will come after a word because “and” is likely the third most popular word in the book. Here’s what came out:
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE.
Second-order approximation works just like bigrams, but instead of letters it uses pairs of words.
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
As Shannon put it, “The resemblance to ordinary English text increases quite noticeably at each of the above steps.”
While all that’s cool, much of it was pretty well known at the time. Shannon had worked on cryptography during World War II and used many of these ideas to encrypt/decrypt messages. Where the leap came was how he used this to think about the quantity of information any message contains. He basically realized that the first example, with 27 random symbols (A-Z plus a space), carried with it much more information than his second- or third-order approximation, where subsequent letters were chosen based on their probabilities. That’s because there are fewer “choices” to be made as we introduce bigrams and trigrams, and “choices”, or lack-thereof, are the essence of information.
Khan Academy has a great video outlining how this works:
[embed]https://www.youtube.com/watch?v=2s3aJfRr9gE[/embed]
Here’s how MIT information theorist Robert Gallager explained the breakthrough:
My kind of study of communication is really a study of transformation, whereas Information Theory and all the existing theories of communication I know of are theories of transportation… Information Theory … has nothing to do with the effects these forms have on you… So mine is a transformation theory: how people are changed by the instruments they employ.
I want to take some time to go through both, as they are fascinating in their own ways.
Transportation
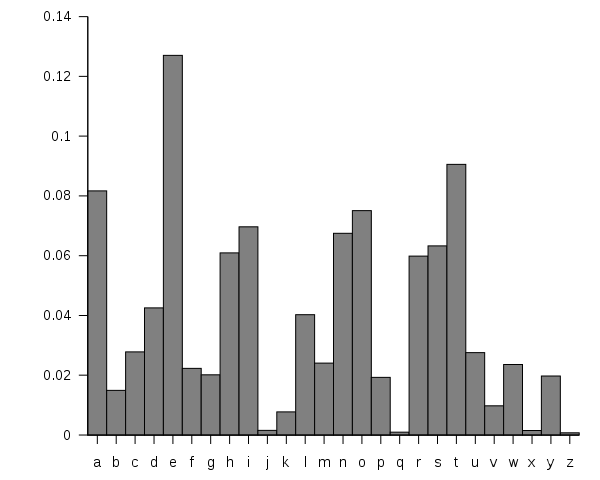
Of course, information existed before Shannon, just as objects had inertia before Newton. But before Shannon, there was precious little sense of information as an idea, a measurable quantity, an object fitted out for hard science. Before Shannon, information was a telegram, a photograph, a paragraph, a song. After Shannon, information was entirely abstracted into bits.- "The bit bomb: It took a polymath to pin down the true nature of ‘information’. His answer was both a revelation and a return" The intellectual leaps Shannon made in his paper "A Mathematical Theory of Communications" were miraculous. What starts off as a question about how to reduce noise in the transmission of information turned into a complete theory of information that paved the way for the computing we all rely on. At the base of the whole thing is a recognition that information is probabilistic, which he explains in a kind of beautiful way. Here's my best attempt to take you through his logic (which some extra explanation from me). Let’s start by thinking about English for a second. If we wanted to create a list of random letters we could put the numbers 1-27 in a hat (alphabet + space) and pick out numbers one by one and then write down their letter equivalent. When Shannon did this he got: XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD But letters aren’t random at all. If you open a book up and counted all the letters you wouldn’t find 26 letters each occurring 3.8% of the time. On the contrary, letters occur probabilistically “e” occurs more often than “a,” and “a” occurs more often than “g,” which in turn occurs more often than “x.” Put it all together and it looks something like this:
So now imagine we put all our letters (and a space) in a hat. But instead of 1 letter each, we have 100 total tiles in the hat and they alight with the chart above: 13 tiles for “e”, 4 tiles for “d”, 1 tile for “v”. Here’s what Shannon got when he did this:
OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL
He called this “first-order approximation” and while it still doesn’t make much sense, it’s a lot less random than the first example.
What’s wrong with that last example is that letters don’t operate independently. Let’s play a game for a second. I’m going to say a letter and you guess the next one. If I say “T” the odds are most of you are going to say “H”. That makes lots of sense since “the” is the most popular word in the English language. So instead of just picking letters at random based on probability what Shannon did next is pick one letter and then match it with it’s probabilistic pair. These are called bigrams and just like we had letter frequencies, we can chart these out.
This time Shannon took a slightly different approach. Rather than loading up a bunch of bigrams in a hat and picking them out at random he turned to a random page in a book and choose a random letter. He then turned to another random page in the same book and found the first occurance of recorded the letter immediately after it. What came out starts to look a lot more like English:
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TUCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE
Now I’m guessing you’re starting to see the pattern here. Next Shannon looked at trigrams, sets of three letters.
For his “third-order approximation” he once again uses the book but goes three letters deep:
IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE
He could go on and on and it would become closer and closer to English. Instead he switches to words, which also occur probabilistically.
For his “first-order approximation” he picks random words from the book. It looks a lot like a sentence because words don’t occur randomly. There’s a good chance an “and” will come after a word because “and” is likely the third most popular word in the book. Here’s what came out:
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE.
Second-order approximation works just like bigrams, but instead of letters it uses pairs of words.
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
As Shannon put it, “The resemblance to ordinary English text increases quite noticeably at each of the above steps.”
While all that’s cool, much of it was pretty well known at the time. Shannon had worked on cryptography during World War II and used many of these ideas to encrypt/decrypt messages. Where the leap came was how he used this to think about the quantity of information any message contains. He basically realized that the first example, with 27 random symbols (A-Z plus a space), carried with it much more information than his second- or third-order approximation, where subsequent letters were chosen based on their probabilities. That’s because there are fewer “choices” to be made as we introduce bigrams and trigrams, and “choices”, or lack-thereof, are the essence of information.
Khan Academy has a great video outlining how this works:
[embed]https://www.youtube.com/watch?v=2s3aJfRr9gE[/embed]
Here’s how MIT information theorist Robert Gallager explained the breakthrough:
Until then, communication wasn’t a unified science ... There was one medium for voice transmission, another medium for radio, still others for data. Claude showed that all communication was fundamentally the same-and furthermore, that you could take any source and represent it by digital data.But Shannon didn't stop there, he goes on to show that all language has redundancy and it can be used to fight noise. The whole thing is pretty mind-blowing and, like I said, underpins all modern computing. (There's a whole other theory about the relationship between information theory and creativity that I'll save for another day.) In part two I'll dive into McLuhan and transformation ... stay tuned (you can subscribe to the RSS feed or email for updates). Also, if you are an information theory expert and find I've misinterpreted something, please get in touch and let me know.